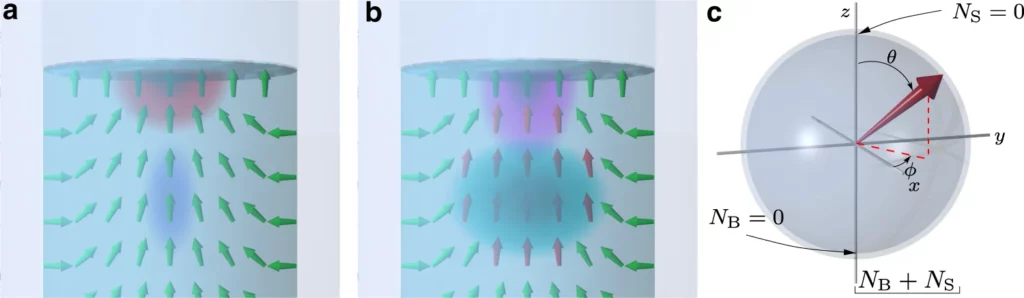
The key distinction of Equation (1) from a conventional two-level Hamiltonian lies in the variable ωB[NB(t)], which stems from a nonlinear feedback mechanism of the spin-orbit trap. This feedback causes the trap to expand with a high local magnon density, altering the distribution of L and consequently reducing ωB. This process, depicted in figure below, in the part b, involves the L distribution being fixed perpendicularly near the surface, keeping ωS relatively constant. As time crystal populations decline, NB decreases, leading to an increase in ωB. By adjusting the initial populations, it’s possible to make the energy levels in the double trap intersect. A detailed explanation of the time crystal wave functions, trapping potential, and feedback mechanism is provided in the Methods section, along with all necessary technical details.
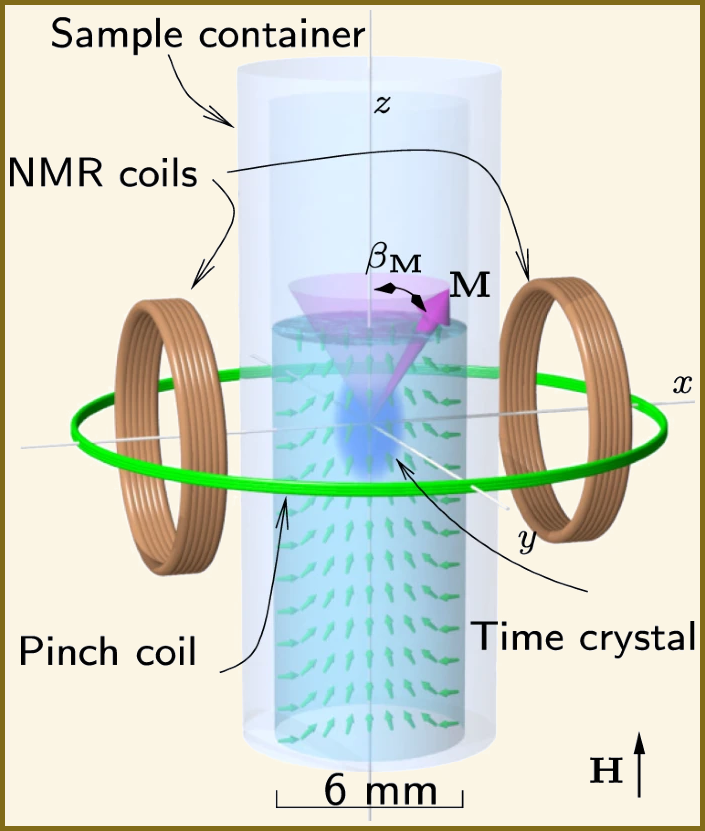
The experiment conducted by Autti et al. involves the innovative trapping of a magnon time crystal inside a quartz glass container. This trapping is achieved through the application of a magnetic field, in conjunction with the utilization of superfluid orbital momentum. The use of a quartz glass container is crucial as it provides the necessary environment for the time crystal while allowing for precise manipulation and observation of its properties through magnetic and superfluid means.
A significant outcome of this study is the demonstration of population transfer and Rabi population oscillations between the time crystals. These phenomena are essential in understanding the dynamic behavior of time crystals and offer insight into how energy and information can be exchanged within such a system. The observation of Rabi oscillations, in particular, suggests a coherent and periodic exchange of populations between different states of the time crystal.
The feedback mechanism and Landau-Zener population transfer are key aspects of this experiment. These concepts are pivotal in quantum mechanics and their application in this context provides a deeper understanding of the non-linear dynamics governing the behavior of time crystals. The feedback mechanism helps in stabilizing the time crystal, while the Landau-Zener model explains how populations shift between different energy levels under varying conditions.
One of the notable results of the study is the observation of the lack of heating under continuous drive, suggesting an efficient energy management within the system. Additionally, the co-existence of time crystals lays bare the many-body interactions for observation, offering a unique window into the complex dynamics and interactions within these exotic states of matter. This aspect is crucial for advancing our understanding of many-body physics in quantum systems.
The study provides valuable insights into the dynamics and coupling between time crystals in the superfluid 3He sample. Understanding how time crystals interact and influence each other in a superfluid environment enhances our comprehension of their collective behavior and potential applications in quantum computing and information processing. The use of superfluid 3He is particularly significant due to its unique quantum properties, which make it an ideal medium for such experiments.
For more detailed information on these groundbreaking findings and their implications, it is recommended to refer to the original document.
Autti, S., Heikkinen, P. J., Nissinen, J., Mäkinen, J. T., Volovik, G. E., Zavyalov, V. V., & Eltsov, V. B. (2022). Nonlinear two-level dynamics of quantum time crystals. Nature Communications, 13(1), Article 3090