Holistic Approach: Bridging Quantum Mechanics and Reality
The Holistic Theory: A Unified View of the Universe
The Holistic Theory merges the principles of quantum mechanics with general relativity, aiming to present a unified and comprehensive understanding of the universe. The theory emphasizes several key areas:
- Physical and Psychological Health: Reflects the immense cosmic scales and spacetime curvature, acknowledging the complex relationship between mental and physical wellness.
- Intellectual & Consciousness Health: Highlights an all-encompassing view where the complex behaviors of quantum particles are intertwined. It positions Intellect and Consciousness as the fundamental pillars that support the Universe’s Information and Quantum Information Fields, laying the foundation for Homo Quanticum Centrism.
- Neuronal & Emotional Health: Stresses the vital role of the observer, suggesting that individual consciousness and emotions could significantly influence reality.
- Science and Spiritual Health: Aligns with the essence of Quantum Centrism, revealing the interconnection between Quantum Technology and Quantum Biology. It bridges the gap between scientific research and spiritual understanding, leading to a deeper appreciation of Intellectual and Emotional Consciousness.
The theory provides a holistic perspective on reality, highlighting the interdependent relationship between Physical, Psychological, Intellectual, Neuronal, Spiritual, and Scientific health, all encapsulated within the concept of Homo Quanticum Centrism.
The Rindler horizon represents a conceptual boundary in spacetime that differentiates regions observable by an observer who is constantly accelerating from those that are forever out of reach. This horizon, akin to the event horizon of a black hole, is not a consequence of the curvature of spacetime but is instead a result of the principles of special relativity. The idea originates from the work of Wolfgang Rindler, who explored the complexities of uniformly accelerating frames in a flat spacetime context [1].
In contrast, the Heisenberg uncertainty principle is a fundamental concept in quantum mechanics. It states that it’s impossible to simultaneously measure the exact position and momentum of a particle with absolute precision. The precision of one measurement inherently compromises the accuracy of the other. This principle ensures that the product of the uncertainties in position and momentum is always greater than a certain fixed value, which is closely related to Planck’s constant. This uncertainty principle is not exclusive to position and momentum but also applies to other pairs of conjugate variables such as energy-time and frequency-time [2].
[1] Wikipedia: Rindler coordinates
[2] Greg Egan, “The Rindler Horizon“
The intersection of the Rindler horizon concept from relativistic physics with the Heisenberg uncertainty principle from quantum mechanics presents some fascinating scenarios. Imagine an observer aboard a perpetually accelerating spaceship, moving away from a source emitting photons of constant frequency. Due to the Doppler effect, the observer will perceive these photons as increasingly redshifted, with their frequency decreasing as they approach the Rindler horizon. In this situation, any attempt by the observer to precisely determine the photon’s position and frequency encounters the Heisenberg constraint, represented by the formula ΔxΔf ≥ c/4π. This means that as the uncertainty in the frequency measurement decreases, the uncertainty in the position measurement increases, and vice versa. This inherent uncertainty prevents the accurate determination of the exact location of the Rindler horizon using photon measurements.
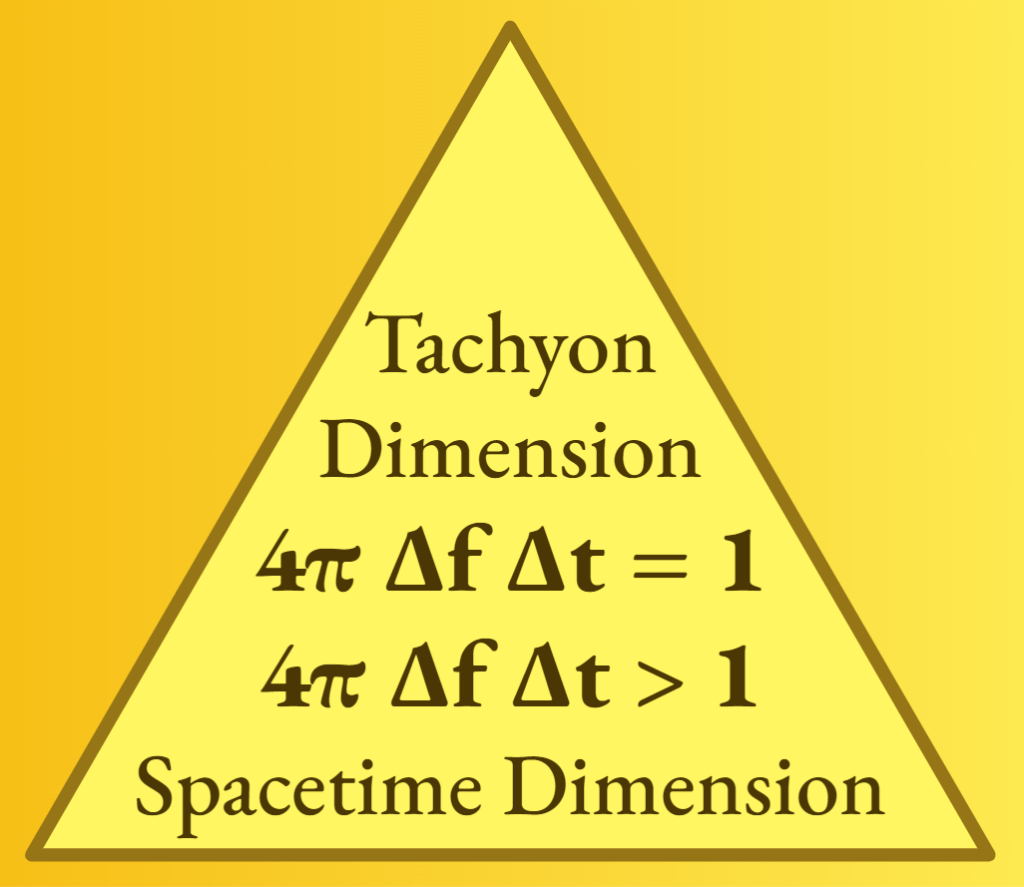
In a similar vein, consider an observer trying to measure the energy-time relationship of a particle as it approaches the Rindler horizon. Here, gravitational redshift would lead to a decrease in the observed energy of the particle as it gets closer to the horizon. Any measurement attempting to pinpoint the energy and time of the particle is constrained by the Heisenberg uncertainty principle, which in this context can be expressed as ΔEΔt ≥ ℏ/2 or equivalently, ΔfΔt ≥ 1/4π. As a result, a decrease in uncertainty in the energy or frequency measurement increases the uncertainty in the time measurement, making it impossible to precisely determine the moment the particle crosses the Rindler horizon.
These examples highlight the complexities and paradoxes that arise when quantum mechanics and relativity intersect, especially under extreme conditions. Understanding these phenomena in their entirety requires a unified theory of quantum gravity, an area that remains one of the most profound challenges in modern physics.
