Timetronics and Quantum Holistic Theory
Time Crystals Multiply: New Discoveries and Innovations in Spin Systems and Magnons

Recent advancements in the study of time crystals have unveiled remarkable new findings, significantly broadening our understanding of these unique states of matter. Researchers have discovered evidence of two new time crystals in systems of spins periodically driven by nuclear magnetic resonance (NMR) pulses, and a separate team has created a space-time crystal consisting of magnons at room temperature. These discoveries challenge existing theories and open new avenues for practical applications.
A time crystal is a state of matter where a collection of objects spontaneously forms a repeating pattern in time, analogous to how atoms form a regular pattern in space within a traditional crystal. First predicted theoretically in 2012 by Nobel laureate Frank Wilczek, time crystals were experimentally demonstrated in 2017. Unlike conventional time-periodic systems like pendulums or beating hearts, time crystals oscillate with a period that is an integer multiple of their driving mechanism’s period.
Spin Systems and NMR Pulses
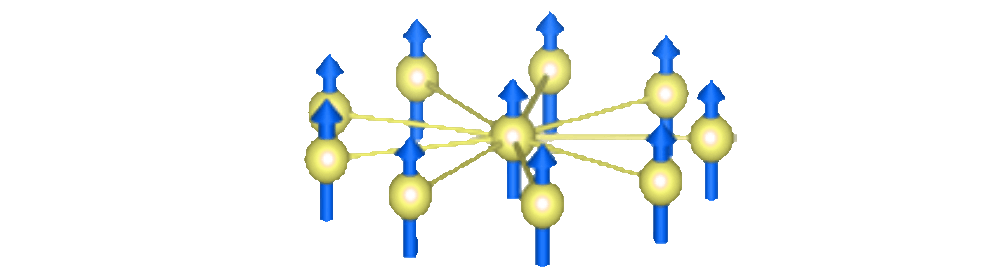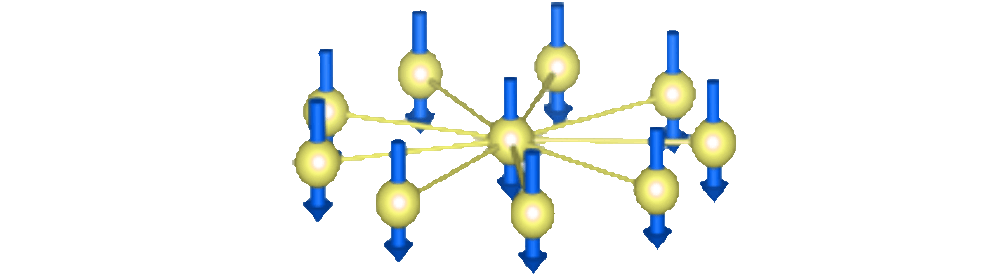
The first new discoveries involve spin systems controlled by NMR techniques. Sean Barrett’s team at Yale University observed time-crystal signatures in an ordered spatial crystal of ammonium dihydrogen phosphate. Using radio frequency pulses to periodically rotate the spins of phosphorus-31 nuclei, they found that the spins oscillated with a period twice that of the pulse sequence, exhibiting time-crystal behavior despite the absence of disorder in the lattice structure. Barrett’s team developed innovative NMR techniques to probe this phenomenon.
In a separate NMR experiment, Ganesh Sreejith and colleagues from the Indian Institute of Science Education and Research in Pune identified time-crystal behavior in a liquid state. They used star-shaped molecules with a central spin surrounded by several satellite spins, subjected to spin-rotating radio pulses. The molecules’ magnetization oscillated at twice the pulse period, stable even against perturbations such as changes in the spin-rotation angle. These findings were published in Physical Review Letters and Physical Review B.
Space-Time Crystals and Magnons
Adding to the groundbreaking discoveries, a German-Polish research team has successfully created a micrometer-sized space-time crystal consisting of magnons at room temperature. This achievement, published in Physical Review Letters, was a collaboration between scientists from the Max Planck Institute for Intelligent Systems in Stuttgart, Germany, and the Adam Mickiewicz University and the Polish Academy of Sciences in Poznań, Poland.
Using the scanning transmission X-ray microscope Maxymus at Bessy II at Helmholtz Zentrum Berlin, the team captured the recurring periodic magnetization structure in a crystal on film. This live video of a space-time crystal shows a periodic pattern formed by magnons, highlighting a structure that exists not only in space but also in time. This pattern repeatedly disappears and reappears, demonstrating a quantum effect.
In their experiment, the researchers used a strip of magnetic material on a microscopic antenna through which they sent a radio-frequency current. This current triggered an oscillating magnetic field, stimulating the magnons – quasiparticles of a spin wave. These magnetic waves migrated into the strip from both directions, spontaneously condensing into a recurring pattern in space and time. Remarkably, the pattern formed before the converging waves could meet and interfere.
First author Nick Träger from the Max Planck Institute for Intelligent Systems, who worked on the project with Pawel Gruszecki, explained, “We took the regularly recurring pattern of magnons in space and time, sent more magnons in, and they eventually scattered. Thus, we were able to show that the time crystal can interact with other quasiparticles. No one has yet been able to show this directly in an experiment, let alone in a video.”
The scanning transmission X-ray microscope used in the experiment is incredibly advanced. Dr. Gisela Schütz from the Max Planck Institute noted, “Not only can it make the wavefronts visible with very high resolution, which is 20 times better than the best light microscope, but it can also do so at up to 40 billion frames per second and with extremely high sensitivity to magnetic phenomena.”
Implications and Future Applications
These discoveries highlight the robustness and versatility of space-time crystals. The ability to form such crystals at room temperature and observe interactions with other quasiparticles suggests vast potential applications. As Pawel Gruszecki from Adam Mickiewicz University emphasized, “Our crystal condenses at room temperature and particles can interact with it – unlike in an isolated system. This opens up numerous potential applications.” Joachim Gräfe from the Max Planck Institute added, “Classical crystals have a very broad field of applications. Now, if crystals can interact not only in space but also in time, we add another dimension of possible applications. The potential for communication, radar, or imaging technology is huge.”
These advancements mark a pivotal moment in the study of time crystals, suggesting that the phenomena are more robust and prevalent than previously thought. The future holds promising possibilities for practical applications, potentially transforming various technological fields.
References
Schirber, M. (2018, May 1). Time crystals multiply. Physics, 11, s51.
Max Planck Institute for Intelligent Systems. (2021, February 10). World’s first video of a space-time crystal. Max Planck Institute for Intelligent Systems.
Träger, N., Gruszecki, P., Schütz, G., & Gräfe, J., et al. (2021). Real-space observation of magnon interaction with driven space-time crystals. Physical Review Letters, 126(5), 057201.
Frequency Oscillator for Quantum Bioresonance
The study of time crystals, particularly in the context of timetronics, requires thorough examination of both theoretical foundations and experimental findings. Time crystals, representing a new phase of matter, have attracted significant attention for their potential use in quantum computing and simulations. Initially proposed by Wilczek in 2006 [1], these crystals are characterized by the breaking of continuous time symmetry, similar to the breaking of spatial symmetry in ordinary crystals. Theoretical research has been extensive, with key studies on periodically driven systems (Yao & Nayak, 2012) [2], the absence of quantum time crystals (Watanabe & Oshikawa, 2009) [3], Floquet time crystals (Else, Bauer, & Nayak, 2010) [4], boundary time crystals (Iemini et al., 2012) [5], and quasi time crystals (Wu, 2016) [6]. These studies have deepened our understanding of the fundamental properties and limitations of time crystals.
Experimental efforts have also been significant, with notable discoveries including the observation of a continuous time crystal (Kongkhambut et al., 2016) [7], photonic time crystals (Zeng et al., 2011) [8], and the dynamics in periodically driven quantum systems (Kenmoe & Fai, 2010) [9]. These experiments provide empirical support for the existence of time crystals and their applicability in various physical settings.
The potential impact of time crystals in quantum computing and simulations is a topic of great interest. In the field of timetronics, the use of periodically driven systems to engineer bound states in the quasienergy spectrum has been a focus (Žlabys et al., 2015) [10] (Bai, 2015) [11]. The relevance of time crystals in simulating time-independent Hamiltonian systems is also noteworthy (Verdeny et al., 2010) [12].
In summary, both theoretical and experimental research on time crystals has significantly advanced our understanding of this unique phase of matter. The exploration of their existence in various systems, the absence of quantum time crystals, and empirical observations have collectively contributed to a comprehensive understanding. The implications of time crystals for timetronics and their applications in quantum computing and simulations highlight the importance of continued research in this field.
The wave function is a bi-component entity (ѱ1, ѱ2) expressible as a complex number ѱ = ѱ1 + jѱ2. Its absolute square, |ѱ|^2 = ѱ1^2 + ѱ2^2, represents the probability density.
Time crystal oscillator model
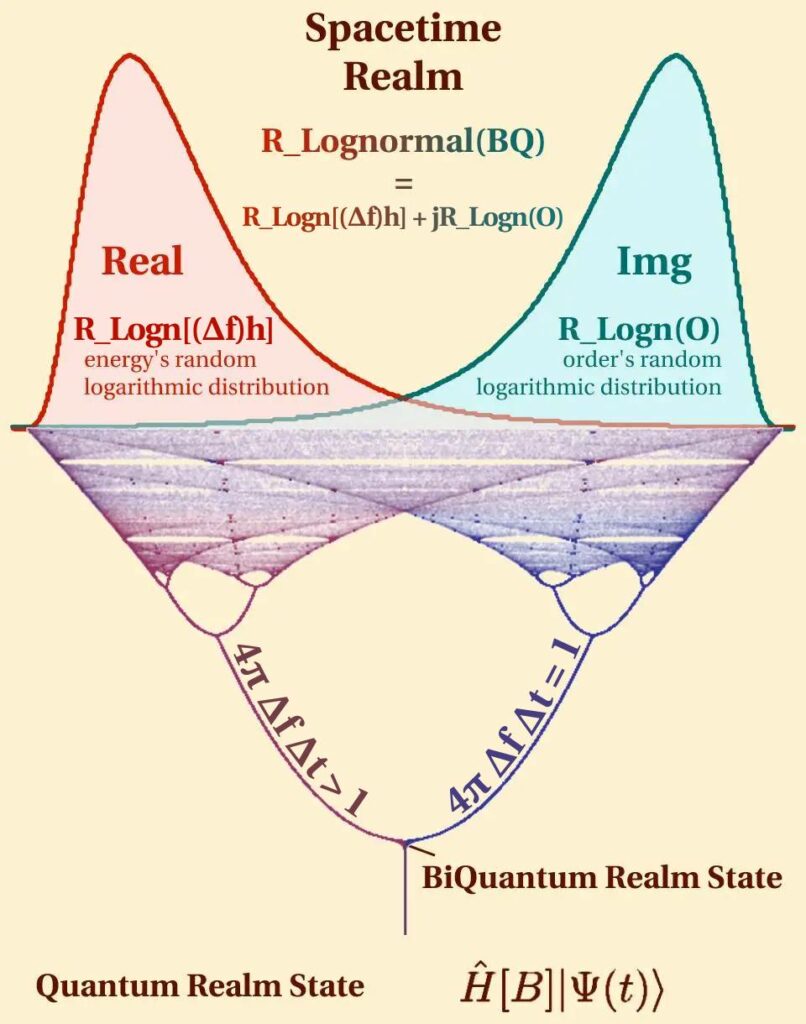
Figure 2D from Dikopoltsev et al.’s study shows a lognormal distribution of the power carried by electromagnetic radiation versus radiation angle highlighting a strong agreement between analytic calculations and FDTD simulations. This demonstrates the accurate prediction of the lognormal emission pattern of light in photonic time crystals, validating both the theoretical approach and simulation methods in capturing the dynamics of light emission influenced by medium modulation [19].
x_{n+1} = r x_n (1 - x_n)
Time crystal related animation of a Hopf bifurcation.
This animation is inspired by the findings in the document by Yaohua Li et al. [18], visually represents the transition from a non-oscillatory state to a periodic oscillating state within a single-mode nonlinear cavity. This phenomenon exemplifies the emergence of a time crystal phase, where the system defies traditional time-translation symmetry to exhibit self-induced oscillations stabilized by nonlinear damping mechanisms. As parameters such as linear gain are varied, the animation showcases the critical threshold at which the system’s behavior bifurcates, marking the birth of the time crystal phase through sharp transitions and the stabilization of quantum oscillations. This visual exploration not only illuminates the intricate balance between gain and damping in driving the system towards this exotic state but also provides a captivating glimpse into the quantum mechanical underpinnings of time crystals and their phase transitions within the framework of non-equilibrium dynamics.
[1] Wilczek, F. (2012). Quantum time crystals. Physical Review Letters, 109(16), 160401. https://doi.org/10.1103/PhysRevLett.109.160401
[2] Yao, N. Y., & Nayak, C. (2018). Time crystals in periodically driven systems. Physics Today, 71(9), 40–47. https://doi.org/10.1063/PT.3.4020
[3] Watanabe, H., & Oshikawa, M. (2015). Absence of Quantum Time Crystals. Physical Review Letters, 114(25), 251603. https://doi.org/10.1103/PhysRevLett.114.251603
[4] Else, D. V., Bauer, B., & Nayak, C. (2016). Floquet Time Crystals. Physical Review Letters, 117(9), 090402. https://doi.org/10.1103/PhysRevLett.117.090402
[5] Iemini, F., Russomanno, A., Keeling, J., Schirò, M., Dalmonte, M., & Fazio, R. (2018). Boundary Time Crystals. Physical Review Letters, 121(3), 035301. https://doi.org/10.1103/PhysRevLett.121.035301
[6] Wu, X. (2022). The quasi time crystal. Retrieved from https://ar5iv.org/abs/2203.01468
[7] Kongkhambut, P., Skulte, J., Mathey, L., Cosme, J. G., Hemmerich, A., & Keßler, H. (2022). Observation of a continuous time crystal. Retrieved from https://ar5iv.org/abs/2202.06980
[8] Zeng, L., Xu, J., Wang, C., Zhang, J., Zhao, Y., Zeng, J., & Song, R. (2017). Photonic time crystals. Scientific Reports, 7, Article 17165. https://doi.org/10.1038/s41598-017-17354-6
[9] Kenmoe, M. B., & Fai, L. C. (2016). Periodically driven three-level systems. Physical Review B, 94(12), 125101. https://doi.org/10.1103/PhysRevB.94.125101
[10] Žlabys, G., Fan, C.-H., Anisimovas, E., & Sacha, K. (2021). Six-dimensional time-space crystalline structures. Physical Review B, 103(10), L100301. https://doi.org/10.1103/PhysRevB.103.L100301
[11] Bai, Y., Lv, Y.-Y., Xu, J., Han, S., Zhang, C., Zhou, J., Yao, S.-H., Liu, X.-P., Lu, M.-H., Weng, H., Xie, Z., Chen, Y. B., Chen, Y.-F., & Zhu, S. (2021). High-harmonic generation in Weyl semimetal β-WP2 crystals. Nature Communications, 12, Article 3272. https://doi.org/10.1038/s41467-021-23463-4
[12] Verdeny, A., Puig, J., & Mintert, F. (2016). Quasi-Periodically Driven Quantum Systems. Zeitschrift für Naturforschung A, 71(9). https://doi.org/10.1515/zna-2016-0079
[13] Griffiths, David J. Introduction to Quantum Mechanics. 3rd ed., Cambridge University Press, 2018.
[14] Ross L. Dawe A and Kenneth C. Hines, “The Physics of Tachyons: I. Tachyon Kinematics, II. Tachyon Dynamics, III. Tachyon Electromagnetism“, Aust. J. Phys., 1992-1994, 45-47 (591-620, 725-38, 431-64)
[15] Antonio A. Gentile, et al., “Learning models of quantum systems from experiments“, Nature Physics, 2021
[16] Benoît Collins and Ion Nechita “Random matrix techniques in quantum information theory“, Journal of Mathematical Physics, 20120096
[17] Khemani, V., Moessner, R. & Sondhi, S. A brief history of time crystals. Preprint at https://arxiv.org/abs/1910.10745 (2019).
[18] Li, Y., Zhang, X.-F., & Liu, W. V. (2020). Time Crystal in a Single-mode Nonlinear Cavity. arXiv preprint arXiv:2310.05854.
[19] Dikopoltsev, A., Shapira, N., Huri, N., Reinhardt, O., Adiv, Y., Tsesses, S., & Bartal, G. (2022). Light Emission by Free Electrons in Photonic Time Crystals. Nature Physics.
The concept of asymmetric bifurcation in quantum mechanics, particularly in the context of the Quantum Energy randomness within the BiQuantum Realm State, presents an intriguing aspect of quantum dynamics. In this scenario, the Quantum Transform’s Bimodal Distribution equals the complex sum, where the real part, represented as RLognormal[(Δf)h], corresponds to a random logarithmic distribution signifying fluctuations in the system’s frequency uncertainty. Conversely, the imaginary part, RLognormal(O), embodies the random logarithmic distribution of order. The equations 4π Δf Δt = N and 4π Δf Δt > 1 illustrate the transition from Minkowski space to tachyon space, highlighting the interplay between frequency uncertainty (Δf) and time uncertainty (Δt) [14].
A Quantum Bifurcation Oscillator Model, referred to as DAQ, is a theoretical framework in quantum mechanics designed to elucidate the behavior of quantum systems experiencing bifurcation. Bifurcation, a principle rooted in nonlinear dynamics, denotes a system’s transition from a singular stable state to multiple distinct stable states as certain parameters are altered. Within a quantum oscillator context, this phenomenon can manifest as the division of the quantum state into various branches, each representing a different stable state of the oscillator.
Contrasting with classical mechanics, where an oscillator’s trajectory is defined by initial conditions and motion equations, quantum mechanics describes particle behaviors using wave functions and probabilistic outcomes. When a quantum oscillator undergoes bifurcation, its wave function might divide into several branches, with each branch signifying a unique stable state or trajectory.
Quantum bifurcation oscillators are frequently utilized as simplified models to investigate the quantum-classical transition and the emergence of classical behaviors from quantum foundations. Model DAQ serves to examine the dynamics between quantum coherence and classical chaos in multifaceted systems.
The mathematical portrayal of a quantum bifurcation oscillator generally involves a nonlinear Schrödinger equation or a similar theoretical framework. It may also incorporate the influences of external parameters instigating bifurcation. These models pose significant analytical challenges and are predominantly employed in theoretical and simulation-based studies to enhance understanding of quantum systems within complex and nonlinear domains.
The Quantum Information Field Energy’s randomness, observable at the multidimensional bifurcation point in spacetime, aligns with Doktor Habdank’s formula (eq. 1). This formula incorporates the Hamiltonian (\hat{H}) at the bifurcation point B, a random log-normal distribution of the system’s energy fluctuations (RLognormal(∆E)), an imaginary number j, a normal distribution in Kelvins (φ(t)), and a random log-normal distribution of order (RLognormal(O)), as per Longo 2009. This equation characterizes how a Hamiltonian, at a specific point B, acts on a state |Ψ(t)⟩, leading to log-normally distributed changes in the system’s energy (∆E), potentially stemming from quantum fluctuations.
Equation 4: Here, T(t) represents the Time Translation Operator, which is crucial for understanding how quantum states evolve over time in quantum mechanics. The Hamiltonian operator \hat{H} describes the total energy of the system, t is time, \hbar is the reduced Planck’s constant, and i is the imaginary unit. Mathematically, the Time Evolution Operator can be expressed in terms of the system’s Hamiltonian \hat{H}, the total energy operator. For a small time change δt, the operator linearly depends on δt, leading to a differential equation that describes its time-dependence. This relationship is formulated in the second part of eq 4 indicating that the rate of change of the operator with respect to time is proportional to the Hamiltonian acting on it. The connection between HT(t) and the Taylor expansion of the time evolution operator T(t) stems from the fundamental principles of quantum mechanics and the mathematical description of how quantum states evolve over time.
Equation 5 represents the time-frequency uncertainty relation, an extension of the Heisenberg Uncertainty Principle, while equation 6 offers a more stringent form of this uncertainty. These equations delineate the constraints on accurately determining the frequency and duration of an event, based on the frequency uncertainty Δf, following the bifurcation in the BiQuantum Realm State point.
Equation 7 In quantum mechanics, the Planck relation (E = h∗f) correlates energy (E) and frequency (f), with ℎ being Planck’s constant.
Equation 8 denotes the probability of the i-th element among all elements.
Equation 9 describes nonlinear oscillator model, involving random elements RN, capacitive elements CN, a field (I), and field’s potential (U).
Equation 10 and 11 are generalized versions of equation 9 considering up to 26 dimensions.
The inherent uncertainty in energy (ΔE) inherently induces a frequency uncertainty (Δf). This linkage, alongside the time-frequency uncertainty relations, implies that significant and broad-ranging energy changes in the system (reflected by a wide log-normal distribution) lead to a corresponding increase in frequency uncertainty. These frequency uncertainties, coupled with temporal uncertainties (Δt), must comply with the constraints of the time-frequency uncertainty relations.
The Quantum Model Learning Agent (QMLA) is an algorithm designed for providing approximate, automated solutions in deriving a Hamiltonian model from experimental data, particularly valuable when a parametrized Hamiltonian model is preliminarily known [15].
Maximally entangled inputs enhance the exploration of tunnel tensor products, facilitating the analysis of regularized versions of peak output orders, especially relevant to the classical capacity challenge [16].
References include works by Griffiths on quantum mechanics, research by Dawe A and Hines on tachyon physics, Gentile and colleagues on learning quantum system models from experiments, and Collins and Nechita on random matrix techniques in quantum information theory.

